It’s time we did a non-pandemic related newsletter issue. So this week we’ll do something more fun. 

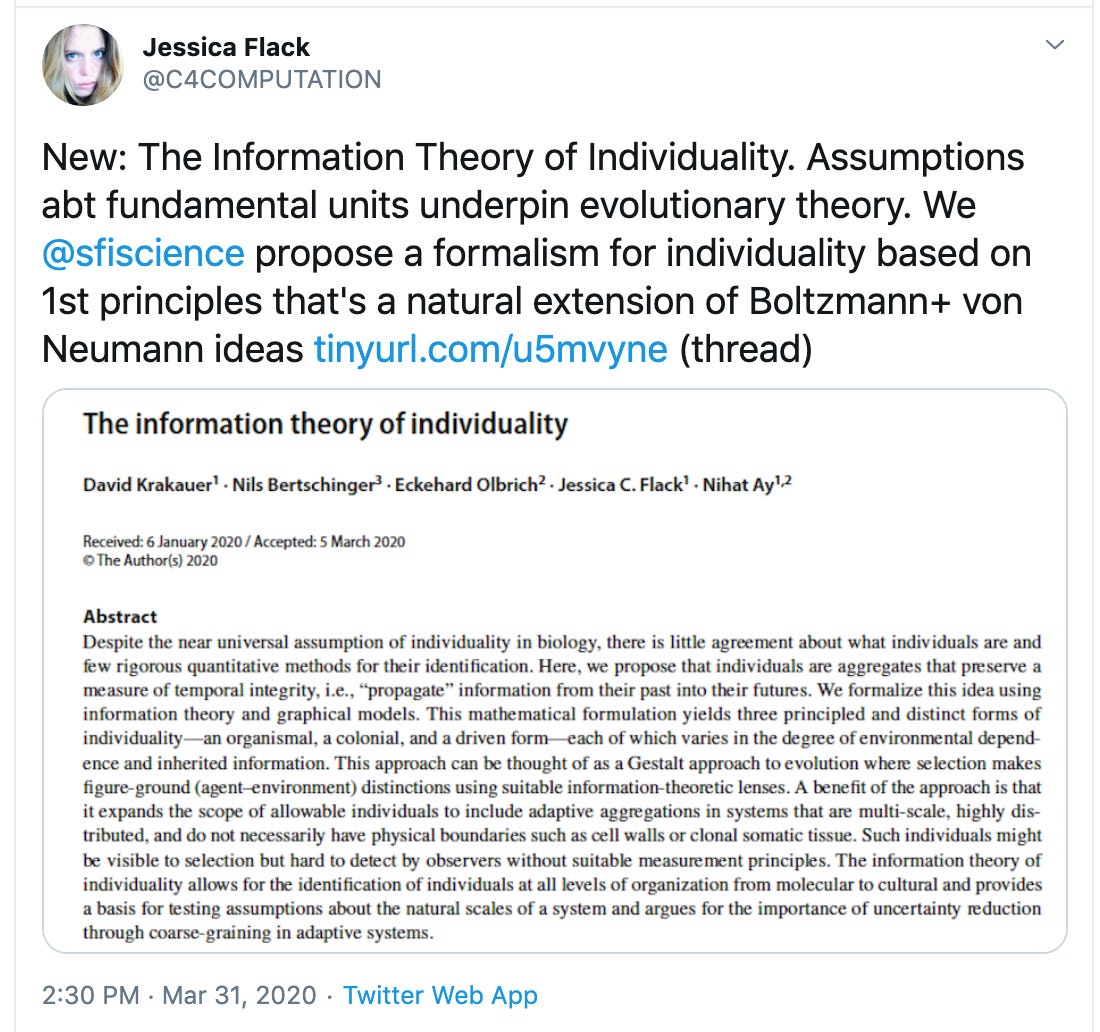
Today we’re going to talk about an interesting journal article that came out two weeks ago, which presents a big idea: formally defining individuality, on a biological level, in terms of information. (Thank you very much to Ethan Buchman for the recommendation.) 

The information theory of individuality | Krakauer, Bertschinger, Olbrich, Flack & Ay,Theory in Biosciences(2020)

I really enjoyed reading this paper, and I hope you enjoy this summary and walkthrough. The paper itself is quite easy to read, the math isn’t bad at all, and I encourage you to read it yourself if you’re interested. Along the way, we’ll have a little math lesson of our own.  And by the end of it, you’ll know what I mean by the cryptic title: “Life is made of unfair coin flips.”

See this Twitter thread, from one of the authors, for an introduction:

For some background, there are two large and related open-ended questions in biology which we’ve debated for a long time, and that we should review first. 

First, there’s the problem of emergence. If you start from biology, it’s pretty easy to work your way backwards by reducing biology into its component parts – you’ll find chemistry and physics as its underlying components, with nothing unaccounted for. But it’s hard to go the other way. Life is a complicated, adaptive, messy thing.  If you start with physics and chemistry, it’s hard to identify what exactly is the thing in here that gives rise to life. We say that life is an “emergent” phenomenon, which lets us dodge the question of “emerges through what, exactly?” 

The second question, which you’ll notice is really the same as the first question just from another angle, is that we have a hard time defining what exactly is an individual. At what point does a collection of molecules comprise an “individual” of some sort? Can we pin it down with a rule that’s defined in terms of the component parts, rather than the behaviour of the emergent product? This has proven to be hard to do.

We’ve uneasily settled on three consensus criteria for biological individuality. First, individuals consume energy and use it to persist and increase in relative frequency. Second, individuals adapt to their environments. Third, the component parts that make up an individual have tightly coordinated relationships with each other. 

All of these should seem pretty sensible. But they aren’t 100% satisfying. They’re proxy observations that don’t yield any deep connection to the underlying chemistry and physics. (Furthermore, they throw up all of these edge cases: a worker ant can’t reproduce; does that mean it’s not an individual? What about viruses?) Can we do better? 

This paper presents a really satisfying idea: the fundamental essence of individuality, and the units in which individuality ought to be measured, is information. You’re dealing with an individual if you’re dealing with “the same thing” between today and tomorrow, and where that sameness isn’t just passive inertia, but is actively propagated. Individuals maximally propagate information from their past to their future. This propagation is measurable, at least in theory. Therefore, individuality ought to also be measurable. 

There are a few nice properties here. This definition of individuality is continuous and measurable, so it embraces the idea that some entities or processes might have more individuality than others. It’s also agnostic to any level of biological organization or abstraction, and furthermore, allows for the concept of nested individuality – the bacteria in our stomachs can possess some level of individuality while still being part the system of us, with its own individuality.

What’s best about this definition is that not only is it rigorously true from first principles, it also establishes a crystal clear link between biology and its reductionist components of chemistry and physics. Information is the link between these two things. That may not feel obvious to some people, so we’re going to go through another important concept you’ve probably heard before but might not totally feel comfortable: entropy. 

Entropy

You were probably introduced to entropy in high school or college chemistry, either in terms of Gibbs Free Energy, or Boltzmann’s kinetic theory of gasses. They’re two ways of looking at the same thing: “disorder.”  

Disorder is a fundamental property of the universe. The second law of thermodynamics, which is one of those ironclad laws of the world, stipulates that total entropy in the universe is always increasing. All living organisms have to continually burn calories and do work to overcome disorder. 

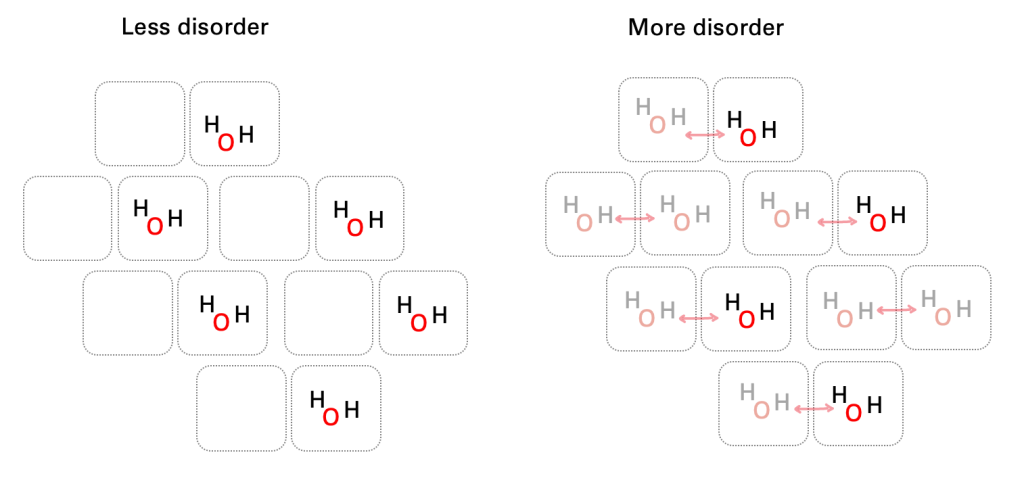
Even reactions that appear to create order (like an ice cube freezing) can only happen if there’s a corresponding release of heat to the outside world, creating on balance an increase in disorder. At a molecular and particle level, the total number of possible “microstates” for any given macrostate (say, water at 5 degrees Celsius) is a manifestation of this disorder: more disorder means more potential states. 

One way to visualize entropy is to imagine an ice crystal in the moment before versus after it melts. In its frozen state, water droplets are fixed in a lattice pattern, where there are empty spaces next to water molecules that are predictably unoccupied. Upon the instant that it melts, those water particles can now occupy either of those positions. The water has become more disordered. 

It’s also possible that you’ve learned about the concept of entropy somewhere else: if you’re an electrical engineer or CS major, you’ve probably learned information theory at some point. Information theory (which we talked about a few weeks ago, in the context of antifragility) is about transmitting information through a noisy channel from a source to a destination. If you remember, information (which we measured in bits) meant the amount of uncertainty there is to resolve, and it often went by another name: entropy. 

This isn’t a coincidence. Both Shannon’s entropy, which is talking about information, and Boltzmann’s entropy, which is talking about thermodynamics, are the same thing. They are a measurement of disorder. 

If you go back to our melting ice crystal example: at the moment our ice melts, the amount of uncertainty in the position of the water molecules increases by one bit per molecule. The information entropy of the water molecule position and the thermodynamic entropy of the melting process are one and the same. Astonishingly, if you do the math on the melting ice cube as a thermodynamic process versus as a communicated message about water molecule position, you get the same answer. I dunno about you but I think this is pretty cool. 

Shannon’s definition of entropy turned out to be a lot more powerful than Boltzmann’s, because it’s so general. “Communication over a noisy channel”, if you generalize it, is the challenge of getting a State to propagate faithfully from A to B, which isn’t just place to place; it’s also over time, or from one process to another. 

Information Theory could be talking about Alice on one end of the phone and Bob on the other end; or it could also mean the sender is your parents, the recipient is you, and the message is the DNA that you inherit from them. Or the sender could be you twenty years ago, the recipient is you today, and the message is that arrangement of neurons and synapses in your brain that have somehow retained every single word of the song No Scrubs by TLC, even though you haven’t heard that song in years. 

So what does it mean for individuals and organisms to propagate information from their past to their future?

Math!

The simplest thought experiment for understanding entropy is a coin flip. When you flip a fair coin, there’s one bit of entropy in the flip – it could be heads or tails; equal probability. When the flip is revealed to be tails, you resolve one bit of information. 

Now imagine that instead of a fair coin, it’s an unfair coin that you know will land on tails every time. If there’s no surprise when it lands tails, then there are zero bits of entropy in the flip. There’s no uncertainty to resolve. What about a slightly unfair coin? There’ll be somewhere between zero bits (minimum amount of uncertainty) and one bit (maximum amount of uncertainty.) The fairness of the coin tells you how “disorder-ful” the coin is. 

It’s worth actually going through the math of an information theory problem in order to really wrap your head around what it means to make a process lower entropy, or “less disorder-ful”. You have the right to skip this next part if you want, but I promise you it’s not scary! It’s elegant and approachable. 

Here is Shannon’s equation:

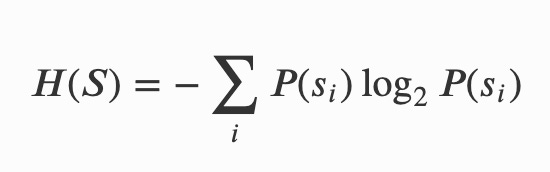
The total amount of entropy in a State H(S) is equal to the sum of:

-The probability of each possible microstate occurring (that’s P(si)); (e.g. “heads” and “tails” are each microstates)

Times

-The number of yes/no questions you’d have to ask, on average, to deduce that particular microstate out of all possible states. That’s the log base 2 part. If you think about this, it’s not scary. Imagine you’re playing a game of twenty questions, and you’re trying to guess out of 8 equal weighted possibilities. If you go about it methodically, it’ll take you 3 guesses: 2 to the 3rd power. -Log base 2 of 1/8th equals 3.

In our fair coin example, it’s trivial: for each side, the probability is .5, and it’d take you one yes/no question to figure it out. So the total amount of entropy is .5 times 1 (heads) + .5 times 1 (tails), or one bit. Which you knew. 

Let’s do a slightly harder one. In our melting ice example, let’s say our ice crystal has twelve possible states, and that they’re equally likely. On average, if you were playing the question game, it would take you 3.58 yes/no questions to correctly guess 1 out of 12. (-Log base 2 of 1/12 is 3.58.) So how “disorderful” is the ice cube? In this case, the math is still easy: it’s 3.58 * 1/12th, times twelve possibilities. So, 3.58 bits of entropy. 

Now let’s change it up a bit. Now we have a new ice cube, still with 12 states, where there are two especially likely states (50% more likely than most!) and two unlikely states (50% as likely). So let’s add it up:

Two states have probability of .125, or 1/8th, which implies on average, it’ll take 3 yes/no questions to figure it out 

Eight states have probability .08333 – on average, 3.58 yes/no questions, same as before

Two states have probability .041666 – on average, 4.58 yes/no questions (lower probability means more questions!)

Let’s add that up: 2 * (.125*3) + 8 * (.0833*3.58) + 2 * (.04166*4.58) = 3.51 bits. 

Now, notice that this number is a little bit smaller! This is important. Our second ice cube is a little bit more like an unfair coin than the first ice cube was. It’s a little bit more predictable, because some microstates are more likely than others. Lower entropy means some microstates are more likely than others, for some predictable reason. 

You might be wondering why Log base 2: why is entropy restricted to uncertainty between two, and only two, choices? Shannon’s paper cleverly resolved this by arguing, look, any uncertainty between more than two choices can be further broken down, like a decision tree, until at some point we get to choices that are sufficiently small that we stop caring past this point. This is called “coarse graining”. It’ll matter in a second. 

Okay, we’re done the math part. You can come back now. 

Mutual Information and the Individual

.  So how do individuals reduce entropy? If you are an individual, or an organism, or some other ordered process, your goal is to get disorder under control – and then keep it that way. 

The last concept to walk through is a concept called mutual information. Mutual information is important whenever the receiver of a message has the opportunity to acquire information from somewhere else. If the receiver of a message already knows something about the message ahead of time, then the message will be less surprising to them. (Imagine guessing the top card of a shuffled deck, versus guessing that top card if you already know that all of the spades have been shuffled to the top. It pays to reduce entropy in advance.)

Mutual information is really important whenever we deal with the question if information propagating from one place to another, or one time to another. If my knowledge about something (like TLC lyrics) stays perfectly consistent as years go by, then we might say there’s total mutual information between the state of me then versus now. On the other hand, lyrics that I’ve totally forgotten mean a mutual information between then and now of zero. 

In a more serious vein, a biological organism does something similar with with respect to every cell, every enzyme, and every metabolic process that it’s made of.

Let’s take an enzyme as an example. A biological enzyme, which catalyzes a chemical reaction in one particular direction, is a bit like an unfair coin. If an enzyme drives a chemical reaction forward in a consistent and predictable way, that’s like a sophisticated version of an unfair coin. It resolves uncertainty about something. Same with DNA and RNA, which pass information forward that reduce uncertainty about a downstream cascade of chemical reactions poised to take place. 

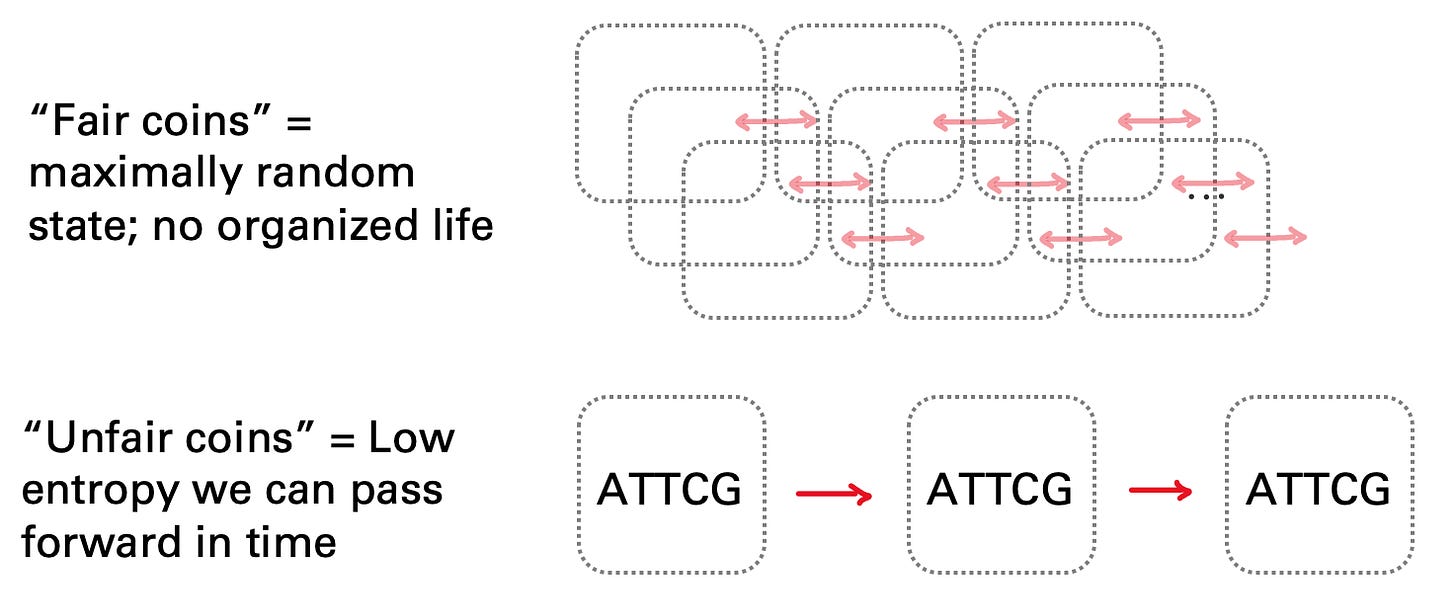
All of the biological stuff you’re made of exists in order to decrease entropy, and then pass that condition forward in time. A simple single-celled organism, even a really stripped-down one, exists in order to pass information forward, in the form of unfair coins. When a process appears to be doing work to actively perpetuate the amount of information that it’s transmitting forward in time, and furthermore, if it’s seeking to maximize that information passed forward, then you’re probably dealing with something we should consider to be an individual. 

In the paper, the authors go through all of the various permutations of Individuals perpetuating mutual information into the future: both internal information, and information that exists with respect to the environment. In all of these cases, whether it’s reproduction, adaptation, or internal self-regulation and metabolism, individuality is a matter of temporal uncertainty reduction. With this new definition, it extends smoothly and easily out of physics and chemistry. As the authors put it: 

What is fundamental in our view is the idea that information can be propagated forward through time [by individuals], meaning that uncertainty is reduced over time. In this way, and returning to our opening remarks…, we suggest individuality is a natural extension of the ideas of Boltzmann and Von Neumann, and as such has foundations in statistical mechanics and thermodynamics, which consider the conditions required for persistently ordered states.

So finally, we can answer: how do organisms pass mutual information forward – either information about themselves, or information about their environments, colony-level information, or all of the above? 

Here’s where we get back to that concept of “coarse graining”: there are certain units of information that are sufficiently “chunked” together, like DNA nucleotides that comprise a genetic code, that they place lower bound on how finely resolved a piece of information must be in order for its fidelity to be maintained. When our DNA is passed forward across cell division or across generations, that information is coarse-grained into A, T, C and Gs. 

Coarse graining allows us to pass mutual information forward, from time today to time tomorrow. We pass that information forward in the form of countless little pieces of unfair coins, like enzymes and nucleotides that make up our metabolic processes and genetic codes, all of which make sure that the uncertainty we’re resolving today is the same as the uncertainty we’re resolving tomorrow. 

Life is made of unfair coin flips, which we propagate forward into the future, in order to make sure our future selves have the same advantage over entropy as we do. I think that’s pretty neat. Hopefully you enjoyed this and learned something from it! If you did, I encourage you again to read the original paper. 

Like this post? Get it in your inbox every week with Two Truths and a Take, my weekly newsletter enjoyed by thousands.